Πως κατασκευάζουμε ένα φράκταλ (von Koch )

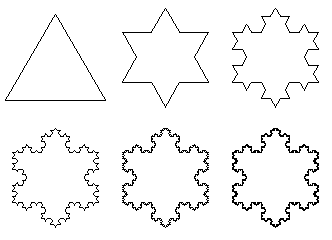
Σχεδιάζουμε ένα ισόπλευρο τρίγωνο και χωρίζουμε την κάθε πλευρά του σε τρία ισα μέρη. 

Με βάση το μεσαίο τμήμα της κάθε πλευράς,  σχηματίζουμε προς το εξωτερικό του τριγώνου ένα νέο ισόπλευρο τρίγωνο και αφαιρούμε την βάση του. Σχηματίζεται έτσι ένα αστεροειδές με 12 πλευρές,  η καθεμία όποιες ισούται με το 1/3 της πλευράς του αρχικού τριγώνου.

Επαναλαμβάνουμε την ίδια διαδικασία στην κάθε πλευρά του νέου σχήματος δημιουργώντας ένα πιο περίπλοκο αστεροειδές με 48 πλευρές. 

Επαναλαμβάνουμε την διαδικασία επ΄ άπειρον , καταλήγουμε σε ένα εξαιρετικά ωραίο και περίπλοκο φρακταλ που φέρει την ονομασία χιονονιφάδα von Koch (παρατήρησε το σχήμα).

Το σχήμα έχει αρκετές απροσδιόριστες ιδιότητες. Αν το αρχικό τρίγωνο είχε πλευρά 1 μονάδα, η περίμετρος του ήταν 3 μονάδες. Αφού σε κάθε νέο βήμα μια πλευρά αντικαθιστάται από τέσσερις νέες πλευρές που έχουν μήκος το 1/3 της αρχικής, η περίμετρος αυτού του νέου σχήματος, θα ισούται με την περίμετρο του προηγούμενου πολλαπλασιασμένη επί 4/3.

Έστι το αρχικό τρίγωνο έχει περίμετρο 3 μονάδες, το πρώτο αστέρι 4, το δεύτερο 16/3 , περίπου 5,33 το επόμενο 64/9=7.11 κ.λ.π. 

Είναι προφανές ότι το τελικό σχήμα θα έχει άπειρη περίμετρο! 

Το εκπληκτικό είναι ότι η άπειρη περίμετρος θα περικλείει ένα πεπερασμένο και σαφώς καθορισμένο εμβαδό. Αποδεικνύεται ότι η χιονονιφάδα του von Koch περικλείει εμβαδό όσο με τα 8/5 του εμβαδού του αρχικού τρίγωνου.

Στο σχήμα που προκύπτει το ίδιο μοτίβο επαναλαμβάνεται ξανά και ξανά. Χονδρικά μπορούμε να ισχυριστούμε ότι τα φράκταλ παρουσιάζεται ως "μαγική εικόνα" που όσες φορές και να μεγεθυνθεί οποιοδήποτε τμήμα του θα συνεχίζει να παρουσιάζει ένα εξίσου περίπλοκο σχέδιο με μερική ή ολική επανάληψη του αρχικού. 

Χαρακτηριστικό επομένως των φράκταλ είναι η λεγόμενη αυτο-ομοιότητα σε κάποιες δομές τους, η οποία εμφανίζεται σε διαφορετικά επίπεδα μεγέθυνσης.

«Ο όρος "φράκταλ" προέρχεται από το λατινικό fractio (θραύσμα, κομμάτι), λόγω της κλασματικής διάστασής του, και πρωτοχρησιμοποιήθηκε από τον Γάλλο μαθηματικό Μπενουά Μάντελμπροτ. Το 1967 ο Μπενουά Μάντελμπροτ έθεσε την φαινομενικά απλοϊκή ερώτηση: «πόσο μεγάλη είναι η ακτογραμμή της Βρετανίας;». 

Ύστερα από σύντομη σκέψη διαπιστώνει κανείς ότι η ερώτηση δεν είναι τόσο απλοϊκή όσο φαίνεται εξαρχής, αφού η απάντηση εξαρτάται από την κλίμακα του χάρτη που χρησιμοποιούμε για να μετρήσουμε την ακτογραμμή! Όσο πιο πολλές λεπτομέρειες έχει ο χάρτης τόσο πιο μεγάλη τιμή για την ακτογραμμή προκύπτει.

Ο λόγος αυτής της παράξενης ιδιότητας είναι ότι η ακτογραμμή είναι ένα φράκταλ. Η γεωμετρία του Ευκλείδη δεν αρκούσε για να περιγράψει τον πραγματικό κόσμο και αυτός είναι ο λόγος που η θεωρία των φρακταλ αντιμετωπίστηκε αρχικά με δυσπιστία.

Την καλύτερη περιγραφή των περίπλοκων αυτών σχημάτων την είχα ακούσει στο πανεπιστήμιο από έναν καθηγητή ο όποιος δήλωνε ότι φράκταλ είναι η γραφική παράσταση μιας συνάρτησης που είναι παντού συνεχής αλλά πουθενά παραγωγίσιμη.

Ο Μάντελμπροτ είναι εκείνος που εισήγαγε τόσο τον όρο όσο και τη θεωρία των φράκταλ στην επιστήμη ,κατόρθωσε να δώσει έναν αρκετά ευρύ αλλά μαθηματικά ακριβή ορισμό τους καθώς και των ιδιαίτερων ιδιοτήτων τους (αυτοομοιότητα, κλασματική διάσταση, μικρή επιφάνεια φράκταλ αλλά άπειρη σε μήκος περίμετρος). θεωρείται ένας από τους σπουδαιότερους μαθηματικούς των τελευταίων 50 ετών.

Περισσότερες λεπτομέρειες στο εξαιρετικό βιβλίο του John Briggs "Fractals: The Patterns of Chaos: Discovering a New Aesthetic of Art, Science, and Nature", καθώς και στο διαδίκτυο το οποίο βρίθει αναφορών και κυρίως φωτογραφιών.

πηγή