«Τα σύννεφα δεν είναι σφαίρες, τα βουνά δεν είναι κώνοι, οι ακτές δεν είναι κύκλοι και ο φλοιός του δέντρου δεν είναι ομαλός, ούτε η αστραπή ταξιδεύει σε μια ευθεία γραμμή!»
Benoit Mandelbrot (The Fractal Geometry of Nature)
Όταν παρατηρείς την φύση, αντιλαμβάνεσαι πως τα πάντα κινούνται και επαναλαμβάνονται με ένα τρόπο κυκλικό. Στην αρχαιότητα όλοι οι πολιτισμοί, γνώριζαν πως στην φύση δεν υπάρχουν ευθείες γραμμές, αντίθετα, παντού κυριαρχούσε η επανάληψη, η κυκλικότητα των μορφών αλλά και των φυσικών φαινομένων.
Ο κύκλος του νερού και της βροχής, ο κύκλος της τροφικής αλυσίδας, οι κυκλικές φωλιές των πουλιών, ο κύκλος της οικογένειας, ο κύκλος των εποχών, κ.λ.π., καθόριζαν και καθορίζουν την ζωή των ανθρώπων σε μεγάλο βαθμό. Στο παρελθόν λόγω της ενότητας και της αλληλεξάρτησης που είχαν οι αρχαίοι πολιτισμοί με την φύση, οι άνθρωποι μπορούσαν να αντιληφθούν την κυκλικότητα και την ενότητας που την χαρακτηρίζει.
Εμείς σήμερα αντίθετα, ζούμε σε ένα μονοδιάστατα γραμμικό κόσμο, όπου κυριαρχούν παντού, οι ευθείες γραμμές και τα τετράγωνα, καταλήγοντας να σκεπτόμαστε επίσης «τετράγωνα και μονοδιάστατα».
Την ιδια στιγμή μέσω των σύγχρονων επιστημών, γνωρίζουμε πως κάθε μορφή στο φυσικό μας περιβάλλον απέχει πολύ από την Ευκλείδεια απλούστευση του γεωμετρικού σχήματος του, το οποίο δημιουργούν οι αισθήσεις μας, ή οι ανάγκες των μετρήσεών μας. Σε κάθε περίπτωση οι φυσικές ευθείες γραμμές σπανίως είναι ευθείες αφού πάντα έχουν κάποιο πλάτος και οι επίπεδες επιφάνειες ποτέ δεν είναι τελείως επίπεδες αφού και το πιο λεπτό φυσικό επίπεδο έχει κάποιο ύψος.
Tα μαθηματικά σχήματα, ο κύκλος, το τρίγωνο, το τετράγωνο, αποτελούν θεωρητικά κατασκευάσματα της Eυκλείδειας γεωμετρίας και σπανίως συναντώνται στη φύση γύρω μας. Και όχι μόνο αυτό. Αυτό που κυριαρχεί στην φύση είναι η επανάληψη, καθώς διάφορα φυσικά μοτίβα επαναλαμβάνονται από τον μικρόκοσμο μέχρι τον μακρόκοσμο.
Κάποια από αυτά τα επαναλαμβανόμενα χαρακτηριστικά μοτίβα είναι λ.χ.: Το ηλιοτρόπιο, το δέρμα της Ζέβρας, οι ομόκεντροι κύκλοι που σχηματίζονται στον κορμό των δέντρων, οι κυψέλες τωνς μελισσών, η χιονονιφάδα, ο ιστός της αράχνης, ο έλικας του D.N.A, και τόσα άλλα. Τα μοτίβα αυτά ονομάζονται «Φράκταλ» (Fractal).
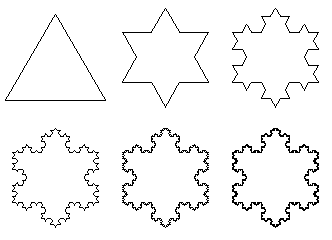
Ο όρος φράκταλ (Fractal), προτάθηκε από τον Μπενουά Μάντελμπρο(Benoît Mandelbrot) το 1975 και προέρχεται από τη λατινική λέξη Fractus που σημαίνει «σπασμένος», «θρυμματισμένος» «κατακερματισμένος». «Φράκταλ» ονομάζεται ένα γεωμετρικό σχήμα που επαναλαμβάνεται αυτούσιο σε άπειρο βαθμό μεγέθυνσης, κι έτσι συχνά αναφέρεται σαν «απείρως περίπλοκο».
Το φράκταλ παρουσιάζεται ως μία «μαγική» εικόνα που όσες φορές και να μεγεθυνθεί οποιοδήποτε τμήμα του θα συνεχίζει να παρουσιάζει ένα εξίσου περίπλοκο σχέδιο με μερική ή ολική επανάληψη του αρχικού. Χαρακτηριστικό επομένως των φράκταλς είναι η λεγόμενη αυτοομοιότητα (self-similarity) σε κάποιες δομές τους, η οποία εμφανίζεται σε διαφορετικά επίπεδα μεγέθυνσης (σχήματα με την ιδιότητα της αυτοομοιότητας). «Αυτοόμοιο» είναι ένα αντικείμενο του οποίου τα μέρη από τα οποία αποτελείται μοιάζουν (είναι όμοια) με το σύνολο (το αντικείμενο).
Αυτή η επανάληψη των ακανόνιστων λεπτομερειών ή σχηματισμών, συμβαίνει προοδευτικά σε μικρότερες κλίμακες και είναι δυνατόν να συνεχίσουν απεριόριστα έτσι ώστε, κάθε τμήμα ενός τμήματος όταν μεγεθυνθεί να μοιάζει βασικά με το συνολικό αντικείμενο. Ουσιαστικά ένα «αυτοόμοιο» αντικείμενο παραμένει αναλλοίωτο σε αλλαγές κλίμακας (όπως επάνω έτσι και κάτω, όπως έξω έτσι και μέσα). Το φαινόμενο αυτό είναι εύκολο να παρατηρηθεί στις νιφάδες του χιονιού, στο φλοιό των δέντρων, στις ακτογραμμές, κ.λ.π.
Φαίνεται ότι τα φράκταλς είναι μια από τις δημιουργικές δυνάμεις στη φύση. Όπως χαρακτηριστικά αναφέρει ο Πλωτίνος στις Εννεάδες: «Τα πάντα βρίσκονται σε μία ενότητα, η οποία έχει την αρχή της στο Έν. Το Όλον έχει την ικανότητα να αναπτύσσεται και να διακλαδίζεται χωρίς να χάνεται το επιμέρους ον εντός του». Σε μία τέτοια συνάρτηση, ο άνθρωπος αποτελεί τμήμα του Όλου, ευρισκόμενος στην ύλη, αλλά αναπολώντας την Ουράνια καταγωγή του. Φανταστήτε για παράδειγμα, την εικόνα του ενός δέντρου στην ανεστραμμένη μορφή του, με τη ρίζα στον ουρανό και τα κλαδιά του στη γη.. .
Οι αρχαίοι Έλληνες φιλόσοφοι και πανεπιστήμονες, με τη γνωστή αδυναμία τους στην τελειότητα της αρμονίας, είχαν δώσει ξεχωριστή σημασία στην «Χρυσή Τομή ή Θεία Αναλογία» και ισούται, περίπου, με 1,62, η οποία σύμφωνα με τον Πυθαγόρα αποτελεί μια από τις κρυμμένες αρμονίες της φύσης.
O Πυθαγόρας παρατήρησε ότι τα φυτά και τα ζώα δεν αναπτύσσονται τυχαία, αλλά σύμφωνα με ακριβείς μαθηματικούς κανόνες. Δεν είναι τυχαία δηλαδή τα όμορφα σχέδια των λουλουδιών. Οι αρχαίοι Έλληνες βρήκαν ότι τα σχέδια των λουλουδιών βασίζονται σε γεωμετρική αναλογία. Επίσης η ακολουθία κάνει την εμφάνισή της στη διάταξη των φύλων γύρω από το μίσχο.
Ο Χρυσός αριθμός θεωρούταν από τους αρχαίους Έλληνες ως η θεϊκή αναλογία όπου η εφαρμογή του σε καλλιτεχνικά δημιουργήματα και κατασκευές οδηγούσε σε «άριστα» και «ωραία» αποτελέσματα. Οι αρχαίοι Έλληνες κατασκεύαζαν σχεδόν όλα τους τα κτίσματα αλλά και τις διακοσμήσεις τους, με τον κανόνα της χρυσής τομής. Ο «Χρυσός Λόγος Φ» ή «Χρυσή Τομή Φ ή Χρυσός Κανόνας Φ ή Θεϊκή Αναλογία» ορίζεται ως το πηλίκο των θετικών αριθμών όταν ισχύει που ισούται περίπου με 1,618.
Η χρυσή τομή συμβολίζεται με το γράμμα Φ προς τιμήν του Φειδία, τον σημαντικότερο γλύπτη της αρχαίας Ελλάδος. Η χρυσή τομή επηρέασε καταλυτικά όλες τις κατασκευές στον αρχαίο ελλαδικό χώρο και όχι μόνο. Στον Παρθενώνα από τα αετώματα και τα σκαλίσματα και τα κιονόκρανα, έως τις Πυραμίδες της Αιγύπτου όλα ακολουθούν τον κανόνα της χρυσής τομής. Ο αριθμός Φ, δίνει αρμονικές αναλογίες και για το λόγο αυτό έχει χρησιμοποιηθεί στην αρχιτεκτονική και τη ζωγραφική, τόσο κατά την Αρχαία Ελλάδα όσο και κατά την Αναγέννηση.
Γιατί όμως και στη Φύση έχει «επιλεγεί» η λογαριθμική σπείρα (είναι το σχήμα που σχηματίζεται σε αυτή την ακολουθία των χρυσών ορθογωνίων,) για να δημιουργηθούν μια πληθώρα από δομές; Οι επιστήμονες έχουν διαπιστώσει με έκπληξη ότι η λογαριθμική σπείρα εμφανίζεται σε σχήματα φυσικών αντικειμένων με εντελώς διαφορετικές ιδιότητες.
Στη μικρότερη κλίμακα εμφανίζεται στα όστρακα πολλών θαλάσσιων οργανισμών, όπως για παράδειγμα είναι ο ναυτίλος. Στην ενδιάμεση κλίμακα εμφανίζεται στο σχήμα των κυκλώνων, όπως αποτυπώνεται χαρακτηριστικά στις φωτογραφίες των μετεωρολογικών δορυφόρων. Τέλος, στη μεγαλύτερη δυνατή κλίμακα εμφανίζεται στο σχήμα των σπειροειδών γαλαξιών, τεράστιων σχηματισμών από εκατοντάδες δισεκατομμύρια αστέρια, τους οποίους μπορούμε να απολαύσουμε στις φωτογραφίες των σύγχρονων τηλεσκοπίων.
Φαίνεται λοιπόν ότι η Χρυσή Τομή αποτελεί έναν αριθμό με παγκόσμιες ιδιότητες, παρόμοιο με τον αριθμό π = 3,14, ο οποίος ισούται με το πηλίκο της περιφέρειας ενός κύκλου διά τη διάμετρό του. Είναι προφανές πως η φύση είναι πολύ πιο σύνθετη και απρόβλεπτη από óτι φανταζόμαστε.Το σύμπαν αναπαράγει τον εαυτό του, είναι απείρως αλληλοσυνδεόμενο και αλληλοεξαρτώμενο.
Σε ένα τέτοιο πλαίσιο θα πρέπει να αντιληφθούμε πως το σύμπαν δεν είναι μονοδιάστατο και γραμμικό, και πως εμείς αποτελούμε ένα αναπόσπαστο απειροελάχιστο τμήμα του. 'Oπως και το σύμπαν, έτσι και στις ανθρώπινες κοινωνίες γινόμαστε ότι σκεφτόμαστε, αναπαράγοντας ένα κόσμο τον οποίο επιθυμούμε, συνεπώς είμαστε κατ΄αυτόν τον τρόπο, συνδημιουργοί του σύμπαντος.
Στον 21 αιώνα η ανθρώπινη φύση είτε θα ρέει σε μία ανεξέλεγκτη πορεία, ακολουθώντας τα θλιβερά γεγονότα που συμβαίνουν πάνω στον πλανήτη, είτε θα κληθεί να αλλάξει ολοκληρωτικά κατεύθυνση. Πλησιάζει η κομβική αυτή στιγμή, όπου όλο και περισσότεροι άνθρωποι θα συνειδητοποιήσουν ότι η πνευματική τους φύση είναι ένα σταθμός ανάμεσα στο χωροχρόνο και στο εικονικό βασίλειο, ανάμεσα στην Γη και στον Ουρανό.
Έως το πρόσφατο παρελθόν ο κόσμος ήταν διασπαρμένος σε εκατομμύρια ξεχωριστά και ασύνδετα φαινόμενα. Οι προσπάθειες για να συνδέσει κανείς αυτά τα φαινόμενα με κάποιου είδους σύστημα, με επιστημονικό ή φιλοσοφικό τρόπο, δεν οδηγούσαν πουθενά, γιατί οι άνθρωποι δεν μπορούσαν να ανασυγκροτήσουν την ιδέα του συνόλου αρχίζοντας από ξεχωριστά γεγονότα, και δεν μπορούσαν μαντέψουν τις αρχές που διέπουν την διαίρεση του συνόλου, χωρίς να γνωρίζουν τους νόμους που διέπουν αυτή την διαίρεση.
Παρά αυτά, η ιδέα της ενότητας των πάντων υπήρχε στην μυστικιστική φιλοσοφική σκέψη, αλλά υπήρχε πάντα ή ανυπέρβλητη δυσκολία της γλώσσας. Βλέποντας την ατέλεια και την αδυναμία της συνηθισμένης γλώσσας, οι άνθρωποι που κατείχαν την μυστικιστική αυτή γνώση, προσπάθησαν να εκφράσουν την ιδέα της ενότητας με μύθους και με σύμβολα.
Αστερισμοί στο Διάστημα και νευρωνικές συνάψεις στον εγκέφαλό μας….
(Πολλά αστέρια μαζί συνθέτουν αστρικά σμήνη τα οποία είναι ζωτικής σημασίας για την ανάπτυξη των γαλαξιών).
Nebula & Ανθρώπινο μάτι..
Σήμερα, παρόλο που δια μέσω της σύγχρονης φυσικής γνωρίζουμε πολύ καλύτερα από παλιά πως ένα φυτό ή ένα ζώο ή ακόμη και ο ίδιος άνθρωπος, στην πραγματικότητα δεν είναι απλά ένας οργανισμός, αλλά ένα σύνολο (δισεκατομμυρίων) συμ-βιωτικών κυττάρων, ή αλλιώς ένα υπερ-πολύπλοκο σύστημα, οι περισσότεροι δυσκολευόμαστε να δεχθούμε ότι σε υποατομικό επίπεδο, το μόνο που υπάρχει είναι ενέργεια.
Στην πραγματικότητα τα άτομα είναι απλά δονούμενη ενέργεια και τίποτα άλλο. Η κβαντική φυσική προχωράει ακόμα παραπέρα, και μας διδάσκει ότι η ενέργεια μπορεί να διαλυθεί στην κενότητα. Ένα κυβικό εκατοστό κενού αγνού μαύρου παγωμένου διαστήματος ενέχει περισσότερη ενέργεια από ότι ένα λαμπρό άστρο. Ανάμεσα στο απειροστά μικρό και στο άπειρα μεγάλο, ανάμεσα στον κόσμο των πρωτονίων, των νετρονίων, των φωτονίων, και στον κόσμο των πλανητικών συστημάτων, των γαλαξιών και των σχηματισμών τους, βρίσκεται η δική μας κλίμακα ζωής, ο δικός μας κόσμος.
Αυτός που συντίθεται από σωμάτια απίστευτα μικρά, από άτομα διαστάσεων 1:10 μέτρα, και που με τη σειρά του συνθέτει μεγακόσμους ασύλληπτων αποστάσεων: Με τους γαλαξίες να έχουν ακτίνα της τάξης των 10 χιλιομέτρων, με το παρατηρήσιμο σύμπαν να εκτείνεται σε μια ασύλληπτα μεγάλη διάμετρο. Από τον κόσμο του σχεδόν απειροστού, οικοδομείται το πεπερασμένο, ο κόσμος της δικής μας κλίμακας, και παραπέρα η απειρότητα των κόσμων.
Σε ένα αλληλοεξαρτώμενο και αλληλοσυνδεόμενο σύμπαν φαντάζει αδιανόητο να μελετήσει κανείς ένα σύστημα του σύμπαντος χωρίς να μελετήσει τον άνθρωπο. Ταυτόχρονα είναι αδύνατον να μελετήσει κανείς τον άνθρωπο χωρίς να μελετήσει το σύμπαν. Ο άνθρωπος είναι μία εικόνα του κόσμου. Δημιουργήθηκε από τους ίδιους νόμους που δημιούργησαν ολόκληρο τον κόσμο.
Tο σώμα μας περιέχει τρισεκατομμύρια κύτταρα.
Kάθε κύτταρο είναι τόσο πολύπλοκο, που χρειάζεται 30.000 κέντρα ανακύκλωσης για να διατηρήσει την πρωτεΐνη που το κρατάει υγιές. Είναι, δηλαδή, σαν να παίρνουμε νεκρά δέντρα, να τα βάζουμε σε ένα μηχάνημα και να μας δίνουν ένα ζωντανό δέντρο , το σώμα μας αποτελείται από κύτταρα, όργανα και συστήματα οργάνων. Aπό την άλλη μεριά, το ίδιο το σώμα αποτελεί κομμάτι ενός ανθρώπου, μιας οικογένειας, μιας κοινότητας, ενός οικοσυστήματος, του κόσμου όλου.
Aν αντιληφθούμε την αξία αυτών των δύο στοιχείων, θα καταλάβουμε ότι κάθε στοιχείο βρίσκεται σε μια συνεχή διαπραγμάτευση με απώτερο σκοπό την εκτόνωση των εντάσεων και τη δημιουργία και διατήρηση ενός σχήματος συνεργασίας που να μπορεί να επιβιώσει. Έτσι, στο σώμα μας, είναι φανερό ότι κάθε ελάχιστη μονάδα (κύτταρο) πρέπει να έχει ισότιμο δικαίωμα στην έκφραση του συμφέροντός του. H συνεργασία και η διαπραγμάτευση αυτών των συμφερόντων δημιουργεί ένα υγιές σώμα.
Αν ο άνθρωπος γνώριζε και καταλάβαινε τον εαυτό του, θα γνώριζε και θα καταλάβαινε ολόκληρο τον κόσμο, όλους τους νόμους που δημιουργούν και κυβερνούν τον κόσμο. Και αντίστροφα, μελετώντας και κόσμο και τους νόμους που κυβερνούν τον κόσμο, θα μάθαινε και θα καταλάβαινε τους νόμους που κυβερνούν τον ίδιο. Γι' αυτό τον λόγο, η μελέτη του κόσμου και η μελέτη του ανθρώπου θα πρέπει να βαδίζουν παράλληλα και η μία να βοηθάει την άλλη. Με τα λόγια του Πλωτίνου :
«Λένε ότι το ένα δεν είναι έξω από κανέναν, είναι παρόν μη αντιληπτό σε όλους…Το να γνωρίσουμε τον εαυτό μας σημαίνει ότι θα γνωρίσουμε την προέλευσή μας».
ΧΛΕΤΣΟΣ ΒΑΣΙΛΗΣ